Отставание времени
Представим, что на расстоянии 864 000 000 км друг от друга находятся две станции. Чтобы пройти это расстояние при скорости 240 000 км/с, понадобится час.
На обеих станциях имеются часы. На первой стации в вагон садится путешественник и перед отходом поезда проверяет свои часы по стационарным. По приезде на другую станцию он с удивлением замечает, что его часы отстали.
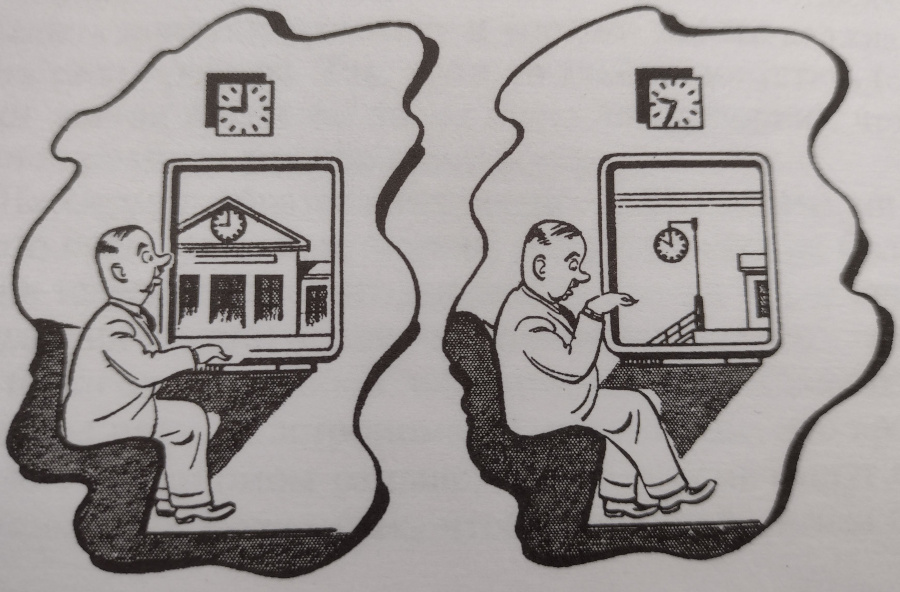
Чтобы разобраться, почему так происходит, представим, что пассажир направляет к потолку луч света от фонарика, поставленного на пол вагона. На потолке расположено зеркало, от которого луч света отражается обратно к лампочке фонарика. Путь луча, каким его увидит пассажир в вагоне, изображен в верхней части рисунка. Совсем иначе выглядит этот путь для наблюдателя, находящегося на платформе. За то время, что луч света пройдет от лампочки до зеркала, само зеркало вследствие движения поезда переместится. Пока луч будет возвращаться, лампочка переместится еще на такое же расстояние.
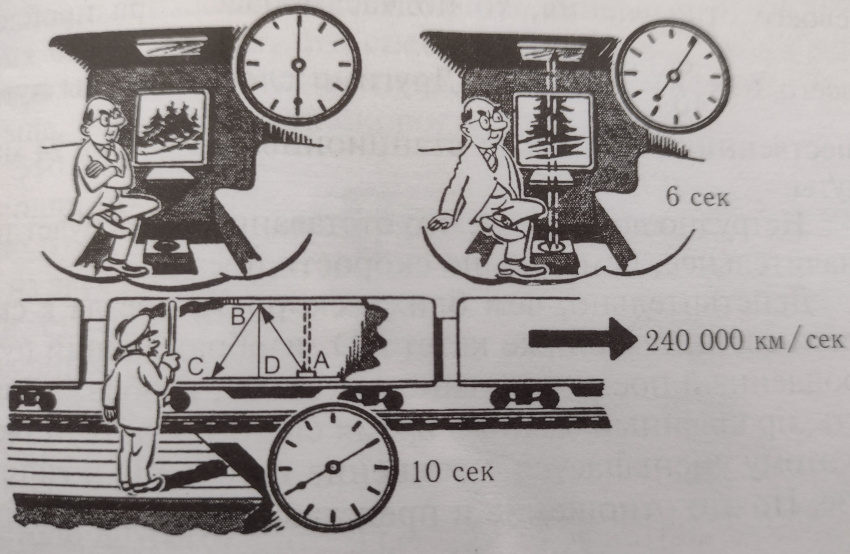
Мы видим, что для наблюдателя на платформе свет прошел явно большее расстояние, чем для наблюдателя в поезде. С другой стороны, мы знаем, что скорость света есть абсолютная скорость, она одинакова и для едущих в поезде, и для тех, кто стоит на платформе. Это заставляет нас сделать вывод: на станции между отправлением и возвращением луча света прошло больше времени, чем в поезде!
Можно вычислить отношение времен. Предположим, наблюдатель на платформе установил, что между отправлением и возвращением луча света прошло 10 секунд. За эти десять секунд свет пробежал 300 000 × 10 = 3 000 000 км. Отсюда следует, что стороны AB и BC равнобедренного треугольника ABC составляют каждая 1 500 000 км. Сторона AC равна пути, пройденному поездом за 10 секунд, то есть 240 000 × 10 = 2 400 000 км.
Теперь легко определить высоту вагона, которая будет высотой BD треугольника ABC.
Вспомним, что в прямоугольном треугольнике квадрат гипотенузы (AB) равен сумме квадратов катетов (AD и BD). Из равенства AB² = AD² + BD² получаем, что высота вагона
Полученная фантастическая высота нас здесь не волнует, так как нам важнее узнать различие во времени при таких скоростях.
Путь, пройденный лучом от пола до потолка вагона и обратно, с точки зрения пассажира равен удвоенной высоте, то есть 2 × 900 000 = 1 800 000 км. Для прохождения этого пути свету понадобится секунд.
Итак, в то время как на станции прошло 10 секунд, в поезде — всего лишь 6 секунд. Значит, если по времени на станции поезд пришел через час после своего отправления, то по часам пассажира пройдет всего минут. Другими словами, часы путешественника отстали от стационарных за час на 24 минуты.
Нетрудно догадаться, что отставание часов будет тем значительнее, чем больше скорость поезда.
Действительно, чем ближе скорость поезда к скорости света, тем ближе катет AD, изображающий путь, пройденный поездом, к гипотенузе AB, изображающей путь, пройденный за то же время светом. Соответственно этому уменьшается отношение катета BD к гипотенузе. Но это отношение и представляет собой отношение времени в поезде и на станции. Приближая скорость поезда к скорости света, мы можем добиться, чтобы за час станционного времени в поезде прошел сколь угодно малый промежуток времени. Так, при скорости поезда, равной 0,9999 скорости света, за час стационарного времени в поезде пройдет лишь одна минута.
Таким образом, всякие движущиеся часы отстают от покоящихся. Не противоречит ли этот результат принципу относительности движения, из которого мы исходили? Не означает ли это, что те часы, которые идут быстрее всех других, находятся в абсолютном покое?
Нет, потому что сравнение часов в поезде с часами на станциях происходило в совершенно неравноценных условиях. Ведь было не двое, а трое часов. Свои часы путешественник сравнивал с двумя разными часами на разных станциях. И наоборот, если бы в переднем и заднем вагонах поезда были вывешены часы, то наблюдатель на одной из станций, сравнивая показания станционных часов с показаниями часов в окнах проносящегося мимо него поезда, обнаружил бы, что систематически отстают станционные часы.
Ведь в данном случае — при равномерном и прямолинейном перемещении поезда относительно станции — мы вправе считать поезд неподвижным, а станцию передвигающейся. Законы природы должны быть одинаковы.
Каждый наблюдатель, неподвижный относительно своих часов, увидит, что спешат другие часы, перемещающиеся относительно него, и забегают вперед тем больше, чем с большей скоростью они движутся.
Это положение аналогично тому, что каждый из двух наблюдателей, стоящих у телеграфных столбов, стал бы утверждать, что его столб виден под большим углом, чем столб другого.
Представим теперь, что поезд движется не по магистрали, а по окружной железной дороге, возвращаясь через определенное время снова к станции отправления. Как мы уже установили, пассажир при этом обнаружит, что его часы отстают, и отстают тем больше, чем быстрее движется поезд. Увеличивая скорость поезда на окружной железной дороге, можно достигнуть такого положения, что за то время как для пассажира пройдет всего-навсего один день, для начальника станции пройдет много лет.
В отличие от путешествия между двумя станциями, когда пассажир проверяет свои часы по разным часам, здесь, при круговом маршруте, сравниваются показания уже не трех часов, а всего лишь двух: часов в поезде и часов на станции отправления.
Нет ли здесь противоречия с принципом относительности? Можно ли считать, что пассажир находится в покое, а станция отправления движется по окружности со скоростью поезда? Ведь тогда мы пришли бы к выводу, что для людей на станции пройдет один день, в то время как для пассажиров пройдет много лет. Такое рассуждение, однако, было бы неверным, и вот почему.
Покоящимся телом можно считать лишь такое, на которое не действуют никакие силы. Правда, существует не один, а бесчисленное множество "покоев", и два покоящихся тела могут, как мы знаем, двигаться относительно друг друга прямолинейно и равномерно. Но на часы в поезде, мчащегося по окружной железной дороге, заведомо действует центробежная сила, и мы поэтому ни в коем случае не можем их считать покоящимися. В этом случае разница между показаниями покоящихся станционных часов и часов в поезде является абсолютной.
Если два человека с часами, показывавшими одно и то же время, разошлись и через некоторое время встретились вновь, то большее время покажут часы того из них, который покоился или двигался равномерно и прямолинейно, то есть те часы, на которые не действовали никакие силы.
Поездка по окружной железной дороге со скоростью, близкой к скорости света, дает нам принципиальную возможность хотя бы в ограниченной степени осуществить "машину времени" Уэллса: выйдя снова на станции отправления, мы обнаружим, что попали в будущее. Правда, на этой машине времени мы можем отправиться в будущее, но лишены возможности вернуться в прошлое. И в этом ее большое отличие от машины времени Уэллса.
Напрасно даже надеяться на то, что дальнейшее развитие науки позволит нам путешествовать в прошлое. Иначе пришлось бы признать принципиально возможными нелепейшие ситуации. В самом деле, отправившись в прошлое, можно было бы очутиться в абсурдном положении человека, родители которого еще не появились на свет.
Путешествия же в будуще таят в себе лишь кажущиеся противоречия.
На небе есть звезды, расположенные от нас, например, на расстоянии, которое луч света проходит за 40 лет. Поскольку мы уже знаем, что движение со скоростью, большей скорости света, невозможно, то позволительно было бы прийти к выводу, что достигнуть этой звезды за промежуток времени, меньший 40 лет, нельзя. Такое умозаключение, однако, ошибочно, так как оно не учитывает изменения времени, связанного с движением.
Предположим, что мы летим на звезду в ракете со скоростью в 240000 км/с. Для жителей Земли мы достигнем звезды через лет. Для нас же, летящих в ракете, это время сократится при упомянутой скорости полета в отношении 10 : 6. Следовательно, мы достигнем звезды не через 50 лет, а через лет.

Увеличивая скорость ракеты, приближая ее к скорости света, можно сколь угодно сокращать время, которое понадобится путешественникам, чтобы добраться до столь отдаленной звезды. Теоретически при достаточно быстром полете можно было бы достичь звезды и вернуться на Землю хоть за одну минуту. На Земле, однако, при этом все равно пройдет 80 лет.