Неприменимость правила сложения скоростей в теории относительности

Какую скорость имеет пассажир относительно полотна железной дороги, если он идет к голове поезда со скоростью 5 километров в час, а поезд движется со скоростью 50 километров в час? Ясно, что скорость человека относительно полотна дороги равна 50 + 5 = 55 км/ч. Рассуждение, которым мы при этом пользуемся, основывается на законе сложения скоростей, и в правильности этого закона у нас не возникает сомнений. В самом деле, за час поезд пройдет 50 километров, а человек в поезде — еще 5 километров. Итого 55 километров, о которых мы говорили.

Вполне понятно, что существование в мире предельной скорости лишает закон сложения скоростей его универсальной применимости к большим и малым скоростям. Ведь если пассажир движется в поезде со скоростью, скажем, 100 000 километров в секунду, то скорость его относительно полотна железной дороги не может быть равной 240 000 + 100 000 = 340 000 километров в секунду, потому что эта скорость превосходит предельную скорость света и, следовательно, не может существовать в природе.

Таким образом, закон сложения скоростей, которым мы пользуемся в повседневной жизни, оказывается неточным. Он справедлив лишь для скоростей, достаточно малых по сравнению со скоростью света.

Несложно понять причины неприменимости, казалось бы очевидного, рассуждения, при помощи которого мы только что вывели закон сложения скоростей. Ведь для этого мы сложили расстояние, пройденное в один час поездом по полотну и пассажиром в поезде. Но теория относительности показывает нам, что эти расстояния складывать нельзя. Это было бы также нелепо, как если бы для того, чтобы определить площадь поля на рисунке ниже, мы перемножили бы длины отрезков AB и BC, забыв, что последний, вследствие перспективы, на рисунке искажен. Кроме того, для определения скорости пассажира по отношению к станции мы должны определить путь, пройденный им за час по станционному времени, в то время как для установления скорости пассажира в поезде мы пользовались поездным временем, что, как нам уже известно, совсем не одно и то же.

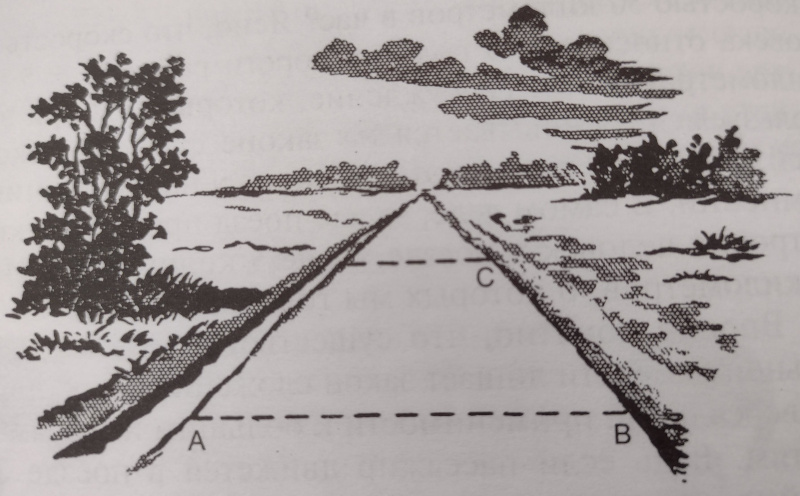
Все это приводит к тому, что скорости, из которых по крайней мере одна сравнима со скоростью света, складываются совсем иначе, чем мы привыкли. Это парадоксальное сложение скоростей можно видеть на опыте, когда мы наблюдаем, например, за распространением света в движущейся воде. То обстоятельство, что скорость распространения света в движущейся воде не равна сумме скоростей света в покоящейся воде и скорости движения воды, а меньше этой суммы, является прямым следствием теории относительности.

Особенно своеобразно складываются скорости в том случае, когда одна из них точно равна 300 000 км/с. Эта скорость, как мы знаем, обладает свойством оставаться неизменной, как бы ни двигались лаборатории, в которых мы ее наблюдаем. Другими словами, какую бы скорость ни прибавить к 300 000 км/с, мы получим опять ту же скорость — 300 000 км/с.

С неприменимостью обычного правила сложения скоростей можно сопоставить следующую аналогию. Как известно, в плоском треугольнике сумма углов A, B, C равняется двум прямым. Представим себе, однако, треугольник, начерченный на поверхности Земли. Вследствие ее шарообразности сумма углов такого треугольника уже будет больше двух прямых. Эта разница становится заметна лишь тогда, когда размеры треугольника сравнимы с размерами Земли.

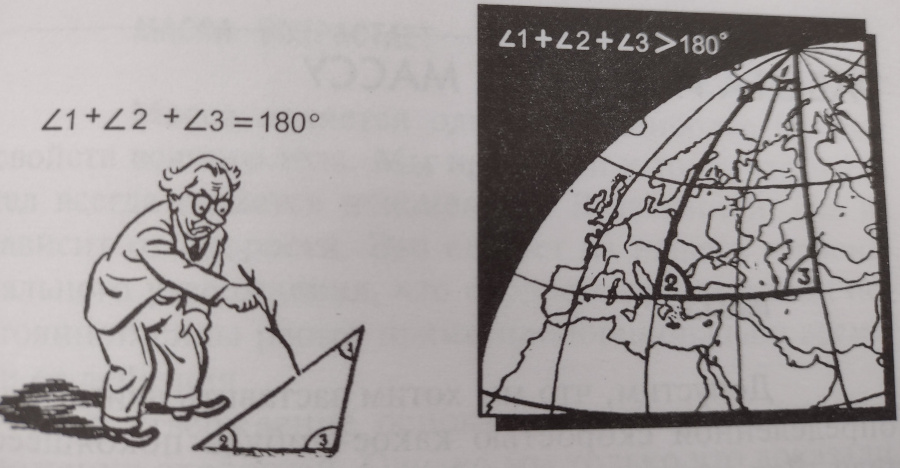
Подобно тому как для измерения площадей небольших участков Земли можно пользоваться правилами планиметрии, так и при сложении небольших скоростей можно пользоваться обычным правилом их сложения.