Свойства степеней с одинаковыми основаниями

Существует три свойства степеней с одинаковыми основаниями и натуральными показателями. Это

• Произведение двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть сумма показателей исходных множителей.
• Частное двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть разность показателей исходных множителей.
• Возведение степени числа в степень равно выражению, в котором основание — это то же самое число, а показатель — это произведение двух степеней.

Будьте внимательны! Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует.

Запишем эти свойства-правила в виде формул:

• a^m × aⁿ = a^m+n
• a^m ÷ aⁿ = a^m–n
• (a^m)ⁿ = a^mn

Теперь рассмотрим их на конкретных примерах и попробуем доказать.

5² × 5³ = 5⁵ — здесь мы применили правило; а теперь представим как бы мы решали этот пример, если бы не знали правила:

5² × 5³ = 5 × 5 × 5 × 5 × 5 = 5⁵ — пять в квадрате — это пять умноженное на пять, а в кубе — произведение трех пятерок. В результате получилось произведение пяти пятерок, но это нечто иное как пять в пятой степени: 5⁵.

3⁹ ÷ 3⁵ = 3^9–5 = 3⁴. Запишем деление в виде дроби:

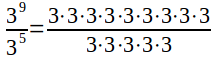
Ее можно сократить:

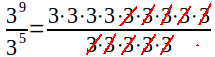
В результате получим:

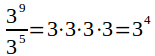
Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать.

Однако при делении нельзя, чтобы делитель был равен нулю (так как на ноль делить нельзя). Кроме того, поскольку мы рассматриваем степени только с натуральными показателями, то не можем в результате вычитания показателей получить число меньше, чем 1. Поэтому на формулу a^m ÷ aⁿ = a^m–n накладываются ограничения: a ≠ 0 и m > n.

Перейдем к третьему свойству:
(2²)⁴ = 2^2×4 = 2⁸

Запишем в развернутом виде:
(2²)⁴ = (2 × 2)⁴ = (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2) = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁸

Можно прийти к такому выводу и логически рассуждая. Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.