Доказать, что гипотенуза больше катета

В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. Почему? На самом деле прийти к такому умозаключению можно несколькими способами.

Во-первых, если знать тот факт, что напротив большего угла всегда лежит большая сторона, и два непрямых угла прямоугольного треугольника острые, то доказательство будет выглядеть совсем просто. Прямой угол равен 90°, и напротив него лежит гипотенуза. Острые углы меньше 90°, значит и лежащие напротив них стороны (катеты) меньше, чем лежащая напротив прямого угла гипотенуза.

Доказательство можно построить по-другому. Пусть дан прямоугольный треугольник ABC с прямым углом A. В таком случае его катетами будут отрезки AB и AC, а гипотенузой отрезок BC.

Проведем в нем на луче BC отрезок BD равный катету AB.

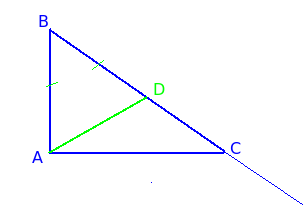
Если AB больше BC, то точка D окажется вне гипотенузы BC, и значит, катет больше гипотенузы. Если же AB меньше BC, то точка D будет лежать на отрезке BC, и это значит, катет меньше гипотенузы.

Рассмотрим треугольник ABD. Он равнобедренный, так как AB = BD по построению. Как известно, в равнобедренном треугольники углы при основании всегда острые. Значит ∠BAD < ∠BAC, так как ∠BAC прямой. Следовательно, луч AD лежит внутри угла ∠BAC и пересекает гипотенузу BC, то есть лежит на ней, а не за ее пределами. Поскольку доказано, что BD < BC, а BD = AB (катету), то значит AB < BC (катет меньше гипотенузы).

Точно также можно доказать, что и катет AC меньше гипотенузы BC, если построить отрезок CD, равный AC.

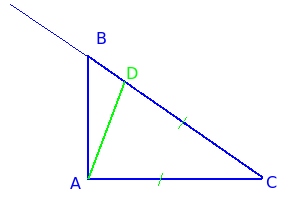
Здесь ∆ADC равнобедренный и ∠DAC < ∠BAC. Следовательно луч AD лежит внутри ∠BAC и пересекает отрезок BC.