Доказать, что перпендикуляр меньше наклонной

Говоря о перпендикуляре имеют в виду, что из какой-либо точки в пространстве проводят перпендикулярную прямую к какой-либо прямой. При этом, понятное дело, точка не должна лежать на прямой, к которой проводится перпендикуляр.

Как известно, из точки, не лежащей на прямой, можно провести только одну перпендикулярную ей прямую. Однако можно провести бесконечное множество прямых не перпендикулярных к заданной прямой и пересекающих ее.

Рассмотрим рисунок:

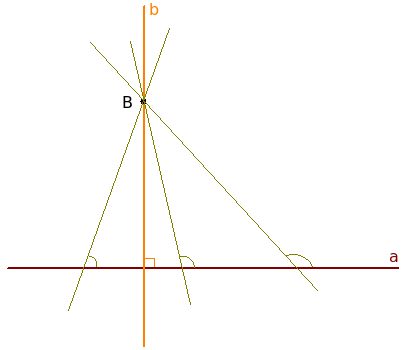
На нем нарисована прямая a и через точку B проведена перпендикулярная ей прямая b. Кроме прямой b через точку B можно провести множество других прямых, пересекающих прямую a, но все они не будут перпендикулярны ей. Все эти прямые называются наклонными.

Существует теорема о том, что любая наклонная, проведенная через заданную точку к прямой, всегда больше перпендикуляра, проведенного через данную точку к прямой. Только обратите внимание, что здесь имеются в виду не прямые, а длины отрезков от точки вне прямой до точек пересечения с ней. Например, на рисунке ниже имеет смысл говорить, что отрезок BA меньше отрезка BC. Но говорить, что прямая b меньше прямой c нельзя, так как прямые бесконечны.

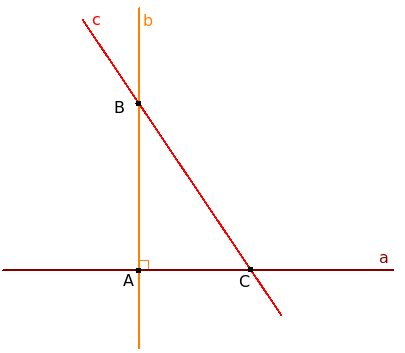
Почему же любая наклонная больше перпендикуляра?

Рассмотрим треугольник ABC. В нем угол A прямой, значит это прямоугольный треугольник. Напротив прямого угла лежит гипотенуза, которая, как известно, всегда больше катета. Поэтому отрезок BC больше отрезка BA, а значит наклонная больше перпендикуляра.

Из того, что перпендикуляр всегда меньше наклонной следует, что кратчайший путь от точки до прямой — это всегда перпендикуляр. Поэтому перпендикуляр еще называют расстоянием от точки до прямой. То есть когда требуется найти расстояние между точкой и прямой имеется в виду отрезок-перпендикуляр к ней.