Что такое каноническое разложение числа и где оно используется?

Каноническим разложением натурального числа на простые множители называют такое его разложение, когда множители записываются в порядке возрастания. Например:
50 = 2 × 5 × 5
124 = 2 × 2 × 31
280 = 2 × 2 × 2 × 5 × 7

Обычно каноническое разложение записывают с использованием степеней:
50 = 2 × 5²
124 = 2² × 31
280 = 2³ × 5 × 7

Общий вид канонического разложения натурального число n имеет вид

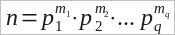
, где p₁ < p₂ < … < p_q.

Каноническое разложение чисел используется при нахождении их наибольших общих делителей (НОД) и наименьших общих кратных (НОК).

НОД(a, b) равен произведению множителей, которые входят в разложение на простые множители обоих чисел, при этом степень показателя у каждого из общих множителей должна быть взята, равной меньшему из показателей, с которым множитель входит в разложение a или b. Например, нам надо найти НОД(50, 280). У разложении чисел 50 и 280 есть два общих множителя – это 2 и 5. При этом наименьшие степени этих чисел равны 1. Поэтому НОД(50, 280) = 2 × 5 = 10.

Аналогично рассуждая, можно найти НОД(124, 280) = 2² = 4.

НОК(a, b) равно произведению множителей (с сохранением степени), которые входят в хотя бы одно разложение чисел на простые множители, умноженных на одинаковые для чисел a и b множители, которые надо взять в наибольшей из встречающихся степеней.

Таким образом, получаем НОК(50, 280) = 2³ × 5² × 7 = 1400, НОК(124, 280) = 5 × 7 × 31 × 2³ = 8680.