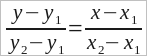Уравнение прямой, проходящей через заданные точки

Если даны две точки, например, A(4; 10) и B(1; 2), то уравнение проходящей через них прямой можно найти, решая систему уравнений.

Если A и B имеют различные первые координаты (абсциссы), то прямая, на которой лежат эти точки, не параллельна оси ординат и описывается уравнением y = kx + b. Далее составляют систему уравнений и решают ее. Например:

Следовательно, уравнение данной прямой имеет вид .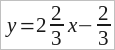

Уравнение прямой можно вывести в общем виде, если выразить его координаты через A(x1; y1) и B(x2; y2). При этом x1 ≠ x2.

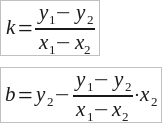
Зная b и k, можно теперь получить уравнение в общем виде:

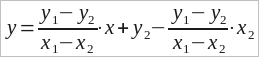
Выполнив алгебраические преобразования, это уравнение можно привести к более простому виду: