Доказательство признаков подобия треугольников

Доказательство первого признака подобия треугольников

Первый признак подобия треугольников утверждает, что если у треугольников две стороны соответственно пропорциональны, а углы между ними равны, то такие треугольники подобны.

Рассмотрим треугольники ABC и DEF, у которых DE = kAB, EF = kBC и ∠B = ∠E.

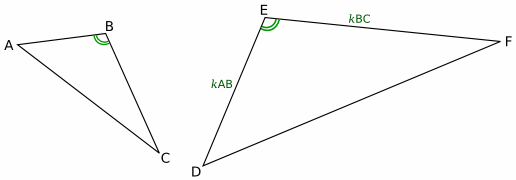
Чтобы доказать подобие данных треугольников, требуется доказать, что DF = kAC, так как подобие треугольников определяется по трем пропорциональным сторонам.

Найдем стороны AC и DF по теореме косинусов (квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон, умноженному на косинус угла между ними):

AC² = AB² + BC² – 2 · AB · BC · cos B
DF² = DE² + EF² – 2 · DE · EF · cos E

Так как ∠B = ∠E и AB = kDE, BC = kEF, то мы можем выразить квадрат стороны DF через угол и стороны треугольника ABC:

DF² = (kAB)² + (kBC)² – 2 · kAB · kBC · cos B

Вынесем k² за скобку:

DF² = k²(AB² + BC² – 2 · AB · BC · cos B)

Выражение в скобках равно ранее выраженному через теорему косинусов квадрату стороны AC. Поэтому можно записать так:

DF² = k²AC²

Отсюда получаем, что DF = kAC, что и требовалось доказать. Таким образом, если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами каждого треугольника равны, то оказываются соответственно пропорциональными и третьи их стороны, а, следовательно, такие треугольника подобны.

Доказательство второго признака подобия треугольников

Второй признак подобия треугольников определяет подобие по наличию двух соответственно равных углов.

Пусть даны треугольники ABC и DEF, у которых ∠A = ∠D, ∠B = ∠E.

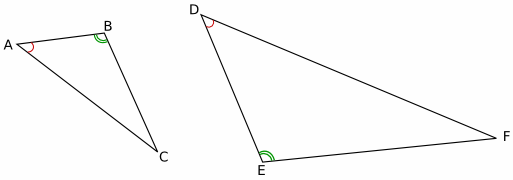
Если эти треугольники подобны, то их стороны будут пропорциональны друг другу, т. е. будут соблюдаться равенства AB = kDE, BC = kEF, AB = kDF.

Если в одном треугольнике два угла соответственно равны двум углам в другом треугольнике, то равными будут и третьи углы этих треугольников, т. к. сумма углов любого треугольника равна 180°.

Как известно, у подобных треугольников углы соответственно равны. Т. е. если треугольники подобны, то их углы соответственно равны. Однако нельзя однозначно утверждать обратное: если углы соответственно равны, то треугольники подобны. Ведь можно предположить, что существую треугольники с соответственно равными углами, но у которых стороны не пропорциональны, а значит, такие треугольники не являются подобными.

Согласно теореме синусов, сторона треугольника равна произведению диаметра описанной окружности на синус противолежащего угла.

Если диаметр описанной около треугольника ABC окружности равен d, то мы можем выразить стороны этого треугольника так:

AB = d sin C, BC = d sin A, AC = d sin B

Если диаметр описанной около треугольника DEF окружности равен d₁, то получим:

DE = d₁ sin F, EF = d₁ sin D, DF = d₁ sin E

Так как углы A, B и C соответственно равны углам D, E и F, то мы можем заменить одни на другие. Сделаем это для сторон треугольника DEF:

DE = d₁ sin C, EF = d₁ sin A, DF = d₁ sin B

Найдем отношения сторон одного треугольника к соответствующим сторонам другого:

AB/DE = (d sin С) / (d₁ sin С) = d/d₁
BC/EF = (d sin A) / (d₁ sin A) = d/d₁
AC/DF = (d sin B) / (d₁ sin B) = d/d₁

То есть все три отношения равны одному и тому же значению (d/d₁), а значит, равны между собой; т. е.

AB/DE = BC/EF = AC/DF

Таким образом, стороны одного треугольника пропорциональны сторонам другого треугольника. Значит, треугольники подобны.

Третий признак подобия треугольников

Нередко выделяют третий признак подобия треугольников: если все стороны одного треугольника соответственно пропорциональны сторонам другого, то такие треугольники подобны. Однако само определение подобных треугольников нередко ограничивается именно этим признаком, а равенство углов подобных треугольников доказывается в виде теоремы (Углы подобных треугольников).