Пересечение медиан треугольника

Существует теорема о том, что медианы треугольника пересекаются в одной точке, и эта точка делит каждую медиану в отношении 2 : 1, где 2 соответствует отрезку от вершины, из которой проведена медиана, до точки пересечения медиан, а 1 соответствует отрезку от точки пересечения медиан до середины стороны, к которой проведена медиана.

Чтобы доказать эту теорему, рассмотрим треугольник ABC с медианами AE, BF, CD. То есть точки D, E, F делят пополам стороны AB, BC, CA соответственно.
Нам не известно, пересекаются ли все медианы в одной точке (это еще требуется доказать). Однако любые две медианы пересекутся в одной точке, так как не могут быть параллельны. Пусть медианы AE и BF пересекаются в точке O.

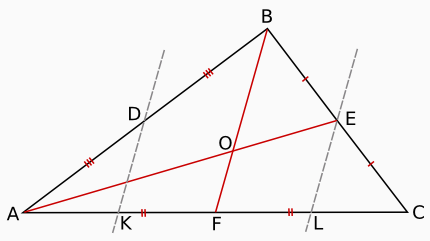
Медиана BF делит медиану AE на два отрезка AO и EO. Проведем через точку E прямую, параллельную BF. Эта прямая пересечет сторону AC в некой точке L. Также проведем через середину отрезка AB (точку D) еще одну параллельную к BF прямую. Она пересечет AC в точке K.

Согласно теореме Фалеса, если на одной стороне угла от его вершины отложить последовательно равные отрезки и провести через концы этих отрезков параллельные прямые, пересекающие другую сторону угла, то эти параллельные прямые отсекут на второй стороне угла также равные между собой отрезки.

Посмотрим на угол BCA данного треугольника. Отрезки BE и EC равны между собой, прямые BF и EL параллельны друг другу. Тогда согласно теореме Фалеса CL = LF.
Если же посмотреть на угол BAC, так как AD = BD и DK || BF, то AK = KF.

Так как отрезки AF и CF равны между собой (т. к. их образует медиана) и каждый из них делится на два равных отрезка, то все четыре отрезка стороны AC равны между собой: AK = KF = FL = LC.

Рассмотрим угол EAC. Через концы трех равных отрезков стороны AC проведены параллельные прямые. Следовательно, они отсекают на стороне AE равные между собой отрезки. Отрезок AO содержит в себе два таких отрезка, а EO только один. Таким образом, мы доказали, что как минимум одна медиана треугольника точкой пересечения с другой медианой делится на два отрезка, длины которых соотносятся как 2 : 1.

Теперь рассмотрим пересечение медианы AE с медианой CD. Пусть они пересекаются в точке P.

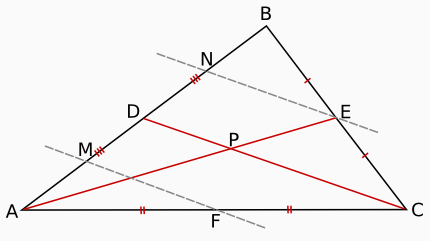
Аналогично предыдущему, доказывается, что параллельные прямые FM, CD, EN делят сторону AB на равные отрезки. В свою очередь они же делят AE на три равных отрезка. Причем от вершины A до пересечения медиан два таких отрезка, а после — один.

Один и тот же отрезок нельзя разделить на три равных части так, чтобы при одном варианте деления они были одного размера, а при другом — другого. Поэтому точки O и P должны совпадать. Это значит, что все три медианы треугольники пересекаются в одной точке.

Чтобы доказать, что две остальные медианы делятся точкой пересечения в соотношении 2 : 1, можно аналогично предыдущему провести параллельные прямые к сторонам AB и BC.