Как зависит парабола от коэффициента
Графиком функции y = x2 является парабола. Данная функция является функцией вида y = kx2, в которой k = 1. Однако какими будут графики функций такого вида при других значениях k?
Графиками всех функций вида y = kx2 также будут являться параболы, но измененные по сравнению с y = x2. При k > 0 чем больше его значение, тем больше значение функции при том же аргументе. Например, при x = 2 функция y = x2 принимает значение y = 4, в то время как значение функции y = 3x2 равно 12, а функции y = 0.5x2 равно 2.
Это значит, что с увеличением значения k (при k > 0) график функции быстрее устремляется вверх, как бы становится круче. Вводят такое понятие как «степень крутизны» параболы.
Если нарисовать графики функций вида y = kx2 при различных значениях k, то возрастание крутизны параболы с возрастанием k можно увидеть наглядно.
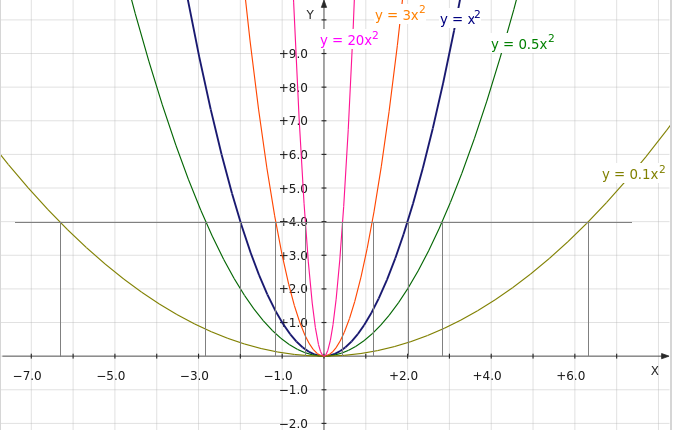
На графике также отмечены точки, соответствующие значению функции, равному 4. Видно, что чем меньше k, тем модуль координаты x больше. Так функция y = 0,1x2 принимает значение, равное 4, при x равном по модулю немного больше 6. А вот функция y = 20x2 принимает то же значение при x равном по модулю меньше 0,5.
Сохранится ли такая же зависимость между коэффициентом k и изменением параболы, если рассматривать функцию вида y = –kx2?
Как известно, функции y = x2 и y = –x2 симметричны друг другу относительно оси x. Поэтому графики функций y = kx2 и y = –kx2 при одинаковых по модулю k также симметричны. Убедимся на графиках:
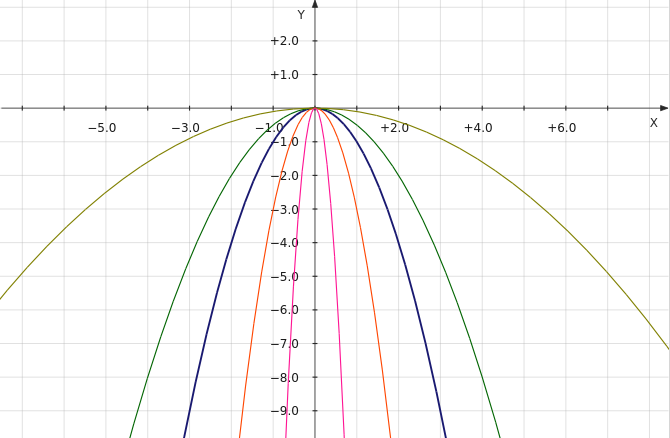
Однако здесь мы не можем сказать, что с увеличением значения k возрастает степень крутизны параболы. Наоборот, она возрастает с уменьшением значения k. Ведь, например, –10 < –1.
Если же говорить о графиках функций вида y = kx при любом значении k (где k — действительное число), то можно сказать, что парабола имеет большую крутизну при большем значении k по модулю (|k|). Ведь |–10| > |–1|.