Доказательство третьего признака равенства треугольников

В третьем признаке равенства треугольников утверждается их равенство по равным трем сторонам. Поэтому требуется доказать, что если у двух треугольников равные стороны, то эти треугольники равны.

Пусть даны треугольники ABC и KLM. В результате измерений было выяснено, что AB = KL, BC = LM, AC = KM.

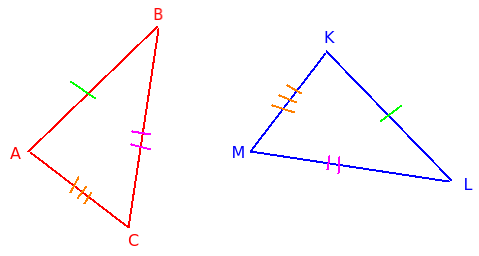
Равны ли эти треугольники?

Совместим два треугольника по их самой длинной стороне так, чтобы получилась симметричная фигура.

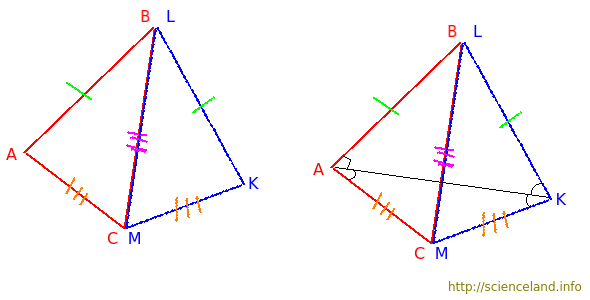
В данном случае совместили стороны BC и LM. По условию они равны друг другу, поэтому совпадают. Вершины A и K находятся по разные стороны от общей стороны. При этом сторона AB симметрична равной ей стороне KL относительно общей стороны BC (LM). То же самое касается сторон AC и KM.

Теперь проведем отрезок AK. Получатся два новых треугольника: AKC (он же AKM) и AKB (он же AKL). Эти треугольники равнобедренные. У ∆AKC AC = KM, у ∆AKB AB = KL.

Как известно, в равнобедренных треугольниках углы при основании равны. Это значит, что в ∆AKC ∠KAC = ∠AKC, а в ∆AKB ∠KAB = ∠AKB. Это значит, что ∠KAC + ∠KAB = ∠AKC + ∠AKB. Но первая сумма это угол A в ∆ABC, а вторая сумма — ∠K в ∆KLM. Значит, ∠A = ∠K.

В треугольниках ABC и KLM соответственно равны стороны AB и KL, AC и KM (по условию задачи). И как мы выяснили, угол A равен углу K.

В соответствии с первым признаком равенства треугольников, если у них равны две стороны и угол между ними, то такие треугольники равны. Значит ∆ABC = ∆KLM.

Таким образом третий признак равенства треугольников был доказан.