Пересечение биссектрис треугольника

Существует теорема о том, что биссектрисы треугольника пересекаются в одной точке.

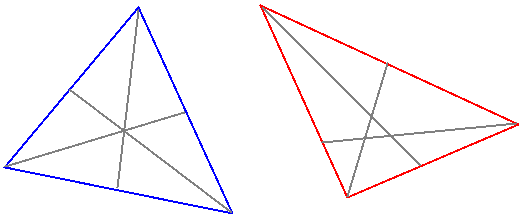
Данный факт, как и всякая теорема, требует доказательства, так как к примеру можно предположить, что биссектрисы треугольника иногда могут не пересекаться в одной точке. На рисунке ниже слева три биссектрисы треугольника пересекаются в одной точке. Справа изображена гипотетическая ситуация, когда каждая биссектриса пересекается с двумя другими в разных точках.

Для доказательства теоремы изобразим две биссектрисы треугольника. Понятно, что они пересекаются в одной точке и других точек пересечения быть не может (т. к. биссектрисы углов одного треугольника не могут быть параллельны друг другу, а любые две прямые всегда имеют точку пересечения, притом только одну). От точки пересечения двух биссектрис проведем три перпендикуляра к сторонам треугольника.

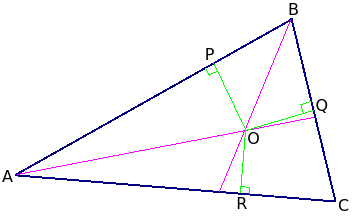
Здесь дан треугольник ABC, изображены биссектрисы его угла A и угла B, которые пересекаются в точке O. От точки O проведены перпендикуляры к сторонам треугольника: ОP ⊥ AB, OQ ⊥ BC, OR ⊥ CA.

Как известно, отрезки-перпендикуляры, проведенные от любой точки биссектрисы угла к сторонам этого угла, равны друг другу. Это следует из равенства прямоугольных треугольников. Например, на рисунке ∆AOP = ∆AOR по общей гипотенузе и равным углам при вершине A (т. к. AO делит угол A пополам).

Значит, OP = OR, так как это перпендикуляры к сторонам треугольника от одной точки биссектрисы AO. Также OP = OQ как перпендикуляры от биссектрисы BO.

Так как OP = OR и OP = OQ, значит OR = OQ. Это означает, что точка O находится на одинаковом расстоянии от сторон BC и CA треугольника. Эти стороны образуют угол C. Как известно, все точки внутри угла, которые равноудалены от его сторон, лежат на биссектрисе этого угла. Значит, точка O лежит на биссектрисе угла C.

Таким образом, биссектриса угла C проходит через точку пересечения биссектрис двух других углов треугольника. Поэтому теорема о том, что биссектрисы треугольника пересекаются в одной точке, доказана.