Формула вершины параболы
Обычно формулу координаты x вершины параболы используют, когда имеют дело с квадратичной функцией.
Квадратичная функция имеет вид: y = ax2 + bx + c.
Ее график — это парабола с вершиной, координаты которой определяются по формулам:
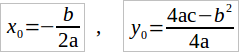
Однако формулу координаты y знать и использовать не обязательно. Обычно проще подставить найденное значение x в саму квадратичную функцию и найти оттуда y.
Например, если дана функция y = 2x2 – 4x + 5, то координата x ее вершины будет равна:
x = –(–4 / (2 × 2)) = 1
Координату же y вычислим, подставив найденный x в саму функцию:
y = 2 × 12 – 4 × 1 + 5 = 3
Таким образом, вершина графика функции y = 2x2 – 4x + 5 находится в точке с координатами (1; 3).
В остальном парабола квадратичной функции вида y = ax2 + bx + c такая же как функции вида y = ax2. Отличие лишь в сдвиге вершины по сравнению с функцией y = ax2. Так в приведенном выше примере y = 2x2 – 4x + 5 парабола будет по форме и направлению ветвей такой же, как для функции y = 2x2. Разница лишь в координатах вершин парабол.
Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата. Как известно функции вида y = f(x + l) + m отличаются от функций y = f(x) сдвигом из графиков по оси x на –l и по оси y на m. Именно l в преобразованной квадратичной функции оказывается равным –b/2a, а m = (4ac – b2) / 4a. То есть l и m — это координаты x0 и y0 соответственно.
Доказывается это применением метода выделения полного квадрата к квадратному трехчлену общего вида ax2 + bx + c. При этом выполняются следующие преобразования:
- Объединим первые два члена многочлена:
y = (ax2 + bx) + c. -
Вынесем коэффициент a за скобку, при этом b разделится на a:
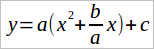
-
Представим, что у нас есть квадрат суммы, в котором x одно из слагаемых, а из выражения в скобках надо получить его полный квадрат суммы. Одночлен
(b/a)xумножим на 2 и разделим на 2 одновременно. Также прибавим и вычтем квадрат второго слагаемого квадрата суммы. Получим: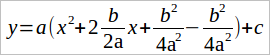
-
Выделим квадрат суммы:
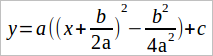
-
Умножим на a:
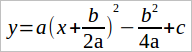
-
Приведем к общему знаменателю свободные члены:
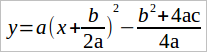
-
Поменяем знак:
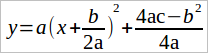
Таким образом, мы привели функцию y = ax2 + bx + c к виду y = a(x + l)2 + m, что соответствует функции y = f(x + l) + m, где f(x) = ax2. А как строить графики последней известно.