Диагонали делятся пополам

Существует теорема о том, что если у четырехугольника диагонали пересекаются и точкой пересечения делятся пополам, то такой четырехугольник является параллелограммом.

Так как параллелограммом по определению является четырехугольник, у которого противоположные стороны равны и параллельны, то значит, надо доказать, что если диагонали четырехугольника делятся пополам, то его противоположные стороны равны и параллельны.

Диагонали четырехугольника могут пересекаться, если этот четырехугольник выпуклый. Значит, нам по условию уже дан выпуклый четырехугольник.

Пусть дан четырехугольник ABCD, его диагонали AC и BD пересекаются и точкой пересечения E делятся пополам. То есть AE = EC и BE = ED. Требуется доказать, что AB = CD и AB || CD, также BC = AD и BC || AD.

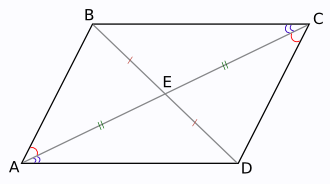
Рассмотрим треугольники AEB и CED. Они равны по двум сторонам и углу между ними: AE = CE, BE = DE (по условию), ∠AEB = ∠CED (как вертикальные). Следовательно, все остальные стороны и углы треугольников соответственно равны.

Стороне AB первого треугольника соответствует сторона CD второго. Значит, AB = CD. Углу BAE соответствует угол ECD, т. е. ∠BAE = ∠ECD. Однако эти углы накрест лежащие при секущей AC. Они могут быть равны, только если AB || CD.

Таким образом, было доказано, что AB = CD и AB || CD.

Если теперь рассмотреть другую пару треугольников (∆BEC и ∆AED), то они также будут равны по двум сторонам и углу между ними. Из этого следует, что BC = AD. Углы BCE и EAD окажутся равными как соответствующие в равных треугольниках. Тогда прямые BC и AD параллельны, т. к. секущая для них AC может образовывать равные накрест лежащие углы только при параллельных прямых.

Следовательно, было доказано, что и вторая пара противоположных сторон равна и параллельна: BC = AD, BC || AD.

То есть если в выпуклом четырехугольнике диагонали, пересекаясь, делятся пополам, то следовательно, у него будут равные и параллельные противоположные стороны, т. е он будет являться параллелограммом.