Доказать чему равна площадь трапеции

Площадь трапеции равна ½ от произведения суммы ее оснований на высоту. Так, если обозначить основания трапеции буквами a и b, высоту — буквой h, то площадь трапеции можно выразить формулой:

S = ½(a + b)h

Напомним, что основания трапеции параллельны. Поэтому высоту можно проводить из любой точки одного основания к прямой, на которой лежит другое основание (или, что чаще, к нему самому).

Обычно теорему о площади трапеции формулируют так: площадь трапеции равна полусумме ее оснований на высоту. Докажем эту теорему.

Рассмотрим трапецию ABCD и проведем в ней диагональ BD, которая разобьет ее на два треугольника ABD и BCD.

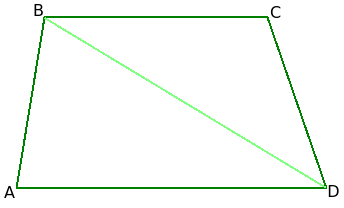
Понятно, что площадь трапеции представляет собой сумму площадей этих двух треугольников.

Площадь любого треугольника равна ½ произведения его основания на высоту (основанием считается сторона, к которой проведена высота). Эта теорема доказывается здесь.

Проведем в треугольниках, полученных из трапеции, высоты к тем сторонам, которые являются также основаниями трапеции. Получатся высоты BH и DI.

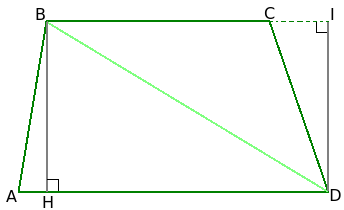
Найдем площади треугольников:

S∆ABD = ½ * AD * BH
S∆BCD = ½ * BC * DI

Высоты треугольников одновременно являются и высотами трапеции. Все высоты трапеции равны между собой (потому что основания трапеции параллельны друг другу). То есть BH = DI, и во втором треугольнике мы можем DI заменить на BH. Тогда, выражая площадь трапеции через площади составляющих ее треугольников, получим:

SABCD = ½ * AD * BH + ½ * BC * BH

Если вынести общие множители за скобки, то как раз получится произведение ½, высоты и суммы оснований:

SABCD = ½ * BH * (AD + BC)