Как построить график кусочной функции

Кусочные функции — это функции, заданные разными формулами на разных числовых промежутках. Например,

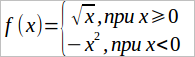
Такая запись обозначает, что значение функции вычисляется по формуле √x, когда x больше или равен нулю. Когда же x меньше нуля, то значение функции определяется по формуле –x². Например, если x = 4, то f(x) = 2, т. к. в данном случае используется формула извлечения корня. Если же x = –4, то f(x) = –16, т. к. в этом случае используется формула –x² (сначала возводим в квадрат, потом учитываем минус).

Чтобы построить график такой кусочной функции, сначала строятся графики двух разных функций не зависимо от значения x (т. е. на всей числовой прямой аргумента). После этого от полученных графиков берутся только те части, которые принадлежат соответствующим диапазонам x. Эти части графиков объединяются в один. Понятно, что в простых случаях чертить можно сразу части графиков, опустив предварительную прорисовку их «полных» вариантов.

Для приведенного выше примера для формулы y = √x получим такой график:

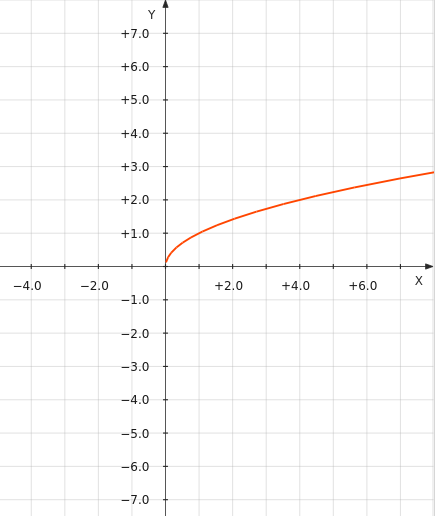
Здесь x в принципе не может принимать отрицательных значений (т. е. подкоренное выражение в данном случае не может быть отрицательным). Поэтому в график кусочной функции уйдет весь график уравнения y = √x.

Построим график функции f(x) = –x². Получим перевернутую параболу:

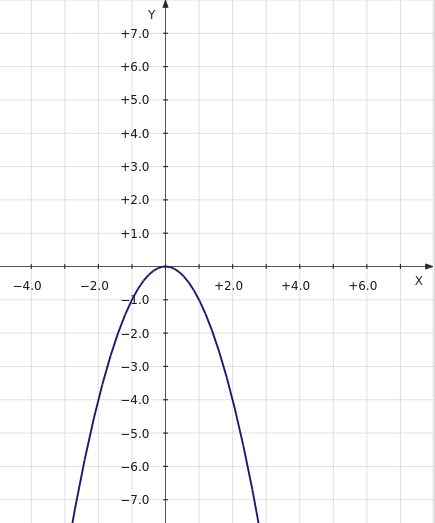
В данном случае в кусочную функции мы возьмем только ту часть параболы, для которой x принадлежит промежутку (–∞; 0). В результате получится такой график кусочной функции:

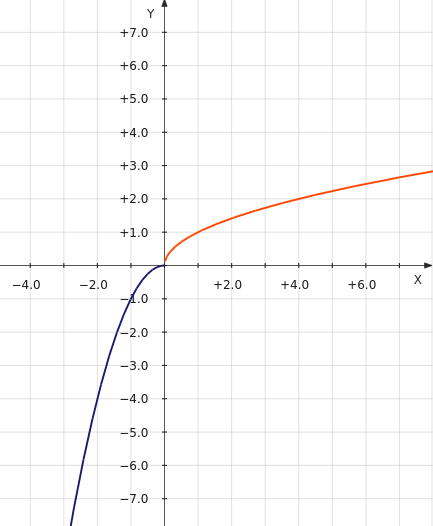
Рассмотрим другой пример:

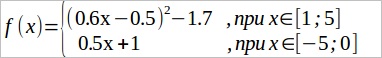
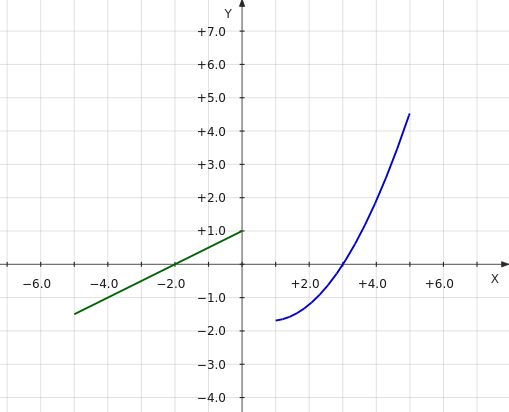
Графиком функции f(x) = (0.6x – 0.5)² – 1.7 будет видоизмененная парабола. Графиком f(x) = 0.5x + 1 является прямая:

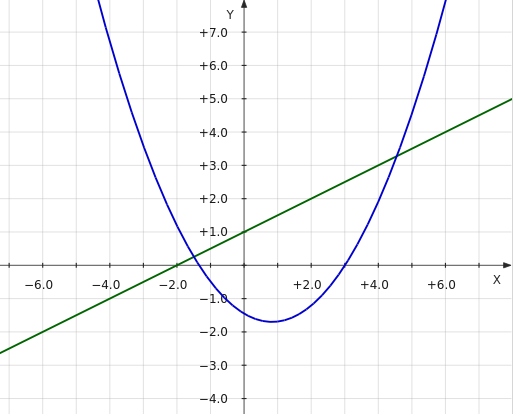
В кусочной функции x может принимать значения в ограниченных промежутках: от 1 до 5 и от –5 до 0. Ее график будет состоять из двух отдельных частей. Одну часть берем на промежутке [1; 5] от параболы, другую — на промежутке [–5; 0] от прямой: