Соотношение между сторонами и углами треугольника

В треугольнике между его сторонами и углами существуют определенные соотношения. Если какой-либо угол треугольника больше другого, то напротив его лежит сторона с большей длиной, чем напротив другого. Другими словами, напротив самого большого угла треугольника лежит самая большая сторона, напротив среднего угла — средняя сторона, а напротив самого маленького угла — самая маленькая сторона.

Понятно, что если углы треугольника равны, то и стороны, напротив которых они лежат, равны.

Сформулировать теорему о соотношениях сторон и углов треугольника можно так: в треугольнике напротив большего угла лежит большая сторона. Однако можно сформулировать обратную ей: в треугольнике напротив большей стороны лежит больший угол.

В прямой теореме нам известны размеры углов, и из этого делается утверждение о размере сторон. А в обратной теореме известны размеры сторон, и делается вывод о размерах углов. Это значит, что при доказательстве прямой теоремы нам дано соотношение углов и требуется доказать соотношение сторон. При доказательстве обратной — дано соотношение сторон, требуется доказать соотношение углов.

Докажем прямую теорему. Пусть дано, что в ∆ABC угол A меньше угла B (∠A < ∠B, или ∠BAC < ∠ABC). Требуется доказать, что сторона, лежащая напротив ∠A, меньше, чем сторона, лежащая напротив ∠B.

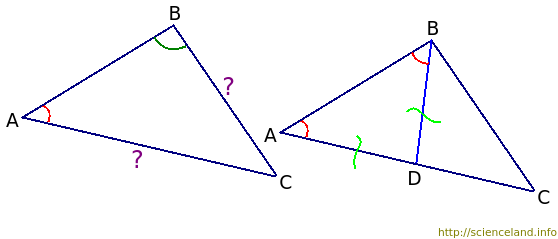
Напротив ∠A лежит сторона BC, а напротив ∠B лежит сторона AC. Требуется доказать, что BC < AC.

Внутри ∠B от стороны AB отложим угол, равный ∠A. Понятно, что этот угол будет меньше, чем ∠B треугольника ABC, так как по условию ∠A < ∠B. Мы откладывали новый угол внутри ∠B, а значит полученная сторона нового угла пройдет внутри ∠B и пересечет сторону AC в некой точке. Назовем эту точку D. Таким образом, мы получили ∠ABD, который равен ∠A.

Поскольку ∠A = ∠ABD, то ∆ABD равнобедренный. У него сторона AD равна стороне BD.

Сторона AC складывается из двух отрезков — AD и CD: AC = AD + CD. Но так как AD = BD мы можем записать, что AC = BD + CD.

Теперь рассмотрим ∆BCD. В нем BD и CD — это две стороны. Третья сторона — это BC. Как известно из теоремы о неравенстве треугольника, любая его сторона меньше суммы двух других. То есть BC < BD + CD. Но BD + CD — это то же самое, что AD + CD или AC.

Значит BC < AC, что и требовалось доказать.