Описанный четырехугольник

Описанный около окружности четырехугольник касается ее всеми своими сторонами. То есть каждая из четырех сторон четырехугольника является касательной к данной окружности. Такая окружности называется вписанной в четырехугольник.

Не каждый четырехугольник можно описать около окружности.

Описанные четырехугольники обладают таким свойством: суммы их противоположных сторон равны. Это значит, что если, около данной окружности описать четырехугольник, например, ABCD, то окажется, что сумма его противоположных сторон AB + СD равна сумме другой пары его противоположных сторон BC + DA.

Чтобы доказать это свойство, возьмем окружность O, опишем около нее произвольный четырехугольник ABCD, обозначим точки касания сторонами четырехугольника окружности буквами K, L, M и N. Также соединим центр окружности с точками касания и центр окружности с вершинами четырехугольника.

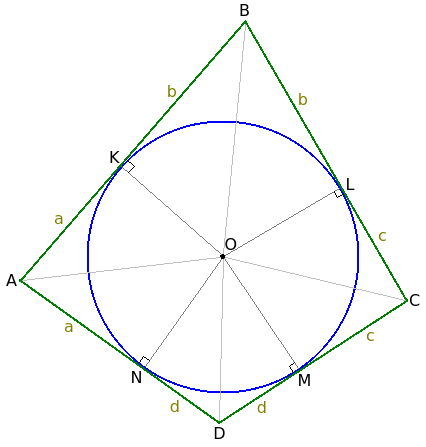
Рассмотрим пары треугольников при каждом угле четырехугольника. При угле A четырехугольника образованы треугольники AOK и AON. Оба эти треугольника прямоугольные, так как радиусы окружности, проведенные к касательной, перпендикулярны ей. Сами радиусы равны друг другу. Оба треугольника имеют общую гипотенузу AO. Одним из признаков равенства прямоугольных треугольников является их равенство по равным гипотенузе и катету. Значит, ∆AOK = ∆AON. Отсюда следует, что сторона AK равна стороне AN. Выразим длину этих сторон буквой a: AK = AN = a.

Аналогично доказывается, что BK = BL, CL = CM, DM = DN. Пусть длина BK = b, CL = c, DM = d.

Сторона четырехугольника AB состоит из отрезков AK и BK: AB = AK + BK. Заменим буквенные обозначения отрезков их длинной: AB = a + b. Аналогично стороны BC = b + c, CD = c + d, DA = d + a.

Теперь через длины выразим суммы противоположных сторон:

AB + CD = (a + b) + (с + d) = a + b + c + d
BC + DA = (b + c) + (d + a) = b + c + d + a = a + b + c + d

В обоих парах противоположных сторон получилась одинаковая сумма, то есть AB + CD = BC + DA. Это и требовалось доказать.

Таким образом, если около окружности описать четырехугольник, то каким бы он ни был, он будет обладать свойством равенства сумм противоположных сторон. Однако из этого еще не следует тот факт, что во всякий четырехугольник, с равными суммами противоположных сторон, можно вписать окружность. На самом деле это так. Этот обратное утверждение называется признаком описанного четырехугольника. Доказательство этого признака выглядит сложнее.