Доказательства свойств модуля

Существуют следующие свойства модуля действительных чисел:

1) |a + b| ≤ |a| + |b|;

2) |ab| = |a| × |b|;

3) , a ≠ 0;

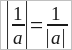4) |a – b| ≥ |a| – |b|.

Проведем доказательства, рассматривая различные случаи значений a и b.

Доказательство 1) |a + b| ≤ |a| + |b|:

Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b. Из этого следует, что |a + b| = |a| + |b|.

Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a|. Выражение же |a| + |b| равно сумме абсолютных значений a и b, что больше, чем b – a. Поэтому |a + b| < |a| + |b|.

Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b|, что также меньше суммы модулей |a| + |b|.

Если a и b – отрицательные числа, то получим |–a – b|. Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b|). Но уже было доказано, что |a + b| = |a| + |b|, следовательно и |–a – b| = |a| + |b|.

Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.

Доказательство 3) 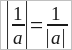, a ≠ 0:

Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/a.

Если a – отрицательное число, то имеем 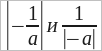. Взятие модуля в обоих выражениях приведет к делению единицы на абсолютное значение a. Значит эти выражения равны друг другу.

Доказательство 4) |a – b| ≥ |a| – |b|:

Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b|, потому что можно не брать модули вообще и тогда с двух сторон получим a – b.

Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b|, что больше, чем |a| – |b|.

Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b|, что больше, чем |a| – |b|.