Накрест лежащие углы при параллельных прямых равны

Существует теорема о том, что прямые параллельны, если при пересечении их секущей накрест лежащие углы оказываются равными. Здесь дано — равные накрест лежащие углы при секущей, следствие — прямые параллельны.

Существует обратная теорема: накрест лежащие углы при секущей равны, если она пересекает параллельные прямые. В данном случае дано — параллельные прямые, следствие — равенство накрест лежащих углов при секущей.

Не является ли обратная теорема «избыточной»? Нельзя ли просто сказать, что только у параллельных прямых накрест лежащие углы при секущей равны? Но может оказаться, эти углы равны и у каких-то не у параллельных прямых. То есть у параллельных они однозначно равны, но есть еще другие прямые, тоже с равными углами. Обратная теорема исключает такую возможность.

Доказательство обратной теоремы сводится к следующему.

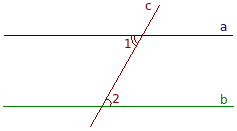
Предполагается обратное, т. е. что при данных параллельных прямых накрест лежащие углы при секущей оказываются не равны. Пусть даны параллельные прямые a и b, которые пересекает секущая c. Предположим, что накрест лежащие углы 1 и 2 не равны друг другу: ∠1 ≠ ∠2.

Через точку пересечения секущей с одной из параллельных прямых (b) проведем прямую d так, чтобы получился равный углу 1 накрест лежащий угол 3: ∠1 = ∠3.

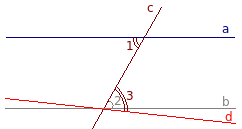
Прямая теорема утверждает, что когда накрест лежащие углы при секущей равны, то прямые параллельны. Значит, прямые a и d параллельны: a || d.

Получается, что через одну точку (в которой пересекаются прямые b, c, d) проведены две параллельные прямые (b и d), которые параллельны прямой a. Однако из ранее доказанной теоремы такого быть не может: через точку, не лежащую на прямой, можно провести только одну параллельную прямую.

Следовательно, предположение о том, что ∠1 ≠ ∠2, не верно. Поэтому ∠1 = ∠2. Нет никакой иной прямой, проходящей через заданную точку, которая давала бы равные углы при секущей, кроме единственной параллельной.