Графически решить уравнение с корнем

Допустим дано такое уравнение:
√x – 0.5x = 0

Требуется решить его графическим способом.

Графический метод решения уравнений заключается в приравнивании двух выражений (частей уравнения), рисования графиков этих выражений-функций на координатной плоскости, нахождения точек пересечения графиков двух функций.

В данном случае преобразуем уравнение к такому виду:
√x = 0.5x

Получаются две функции, чьи графики следует изобразить на координатной плоскости:
f(x) = √x
g(x) = 0.5x

Первый график — это ветвь параболы, вытянутая вдоль оси x. Второй график — прямая.

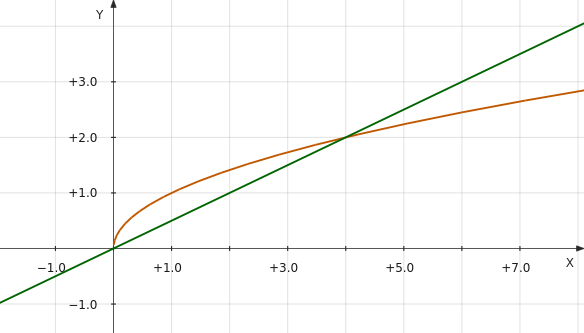
Как видно из построения, графики функций пересекаются в двух точках: (0; 0) и (4; 2). Нас интересует только координата x. Значит уравнение √x – 0.5x = 0 имеет два корня: x₁ = 0 и x₂ = 4.

Действительно, если подставить в уравнение определенные по графикам значения x, то левая и правая части уравнения будут равны друг другу.

Решим графически такое уравнение:
√x = (0.6x−3.3)² − 4

Здесь в качестве графиков функций имеем параболу и ветвь параболы:

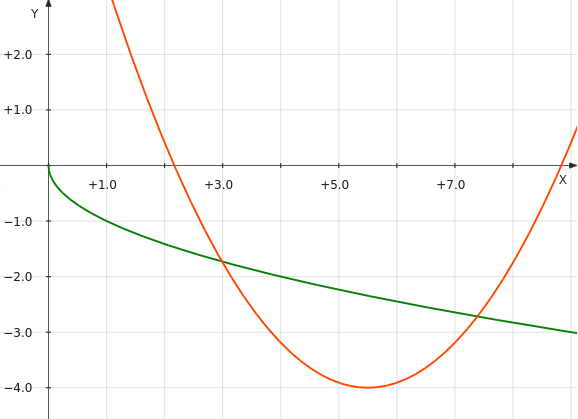
Графики функций, как и в первом случае, пересекаются в двух точках. Однако точно определить точки пересечения нельзя. Можно лишь сказать приблизительно, чему будут равны корни такого уравнения. Одна точка пересечения графиков — это примерно (3; –1.7), вторая точка имеет примерные координаты (7.4; –2.7). Таким образом, x₁ ≈ 3, x₂ ≈ 7.4.

Следует отметить, что графики функций какого-либо заданного уравнения могут пересекаться только в одной точке. В таком случае, уравнение имеет только один корень. Если графики вообще не пересекаются, то уравнение не имеет корней.