Если накрест лежащие углы при секущей равны, то прямые параллельны

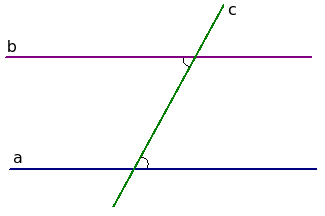
Пусть даны две прямые a и b, которые пересекаются прямой c. То есть прямая c является секущей для прямых a и b. При этом образуются две пары накрест лежащих углов. Если в любой из этих пар углы равны, то прямые a и b параллельны. На чертеже обозначена одна пара равных между собой накрест лежащих углов.

Дано (условие). Равенство накрест лежащих углов.

Следствие (утверждение; то, что требуется доказать). Параллельность прямых.

Формулировка в виде теоремы. Если при пересечении двух прямых секущей накрест лежащие углы оказываются равны, то значит, эти прямые параллельны.

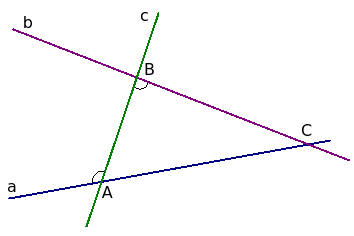
Доказательство. Воспользуемся методом от противного. Пусть накрест лежащие углы равны, но предложенные прямые не параллельны. Если прямые не параллельны, то они пересекутся в одной точке. На чертеже секущая c пересекает прямые a и b в точках A и B, а сами прямые пересекаются в точке C.

В результате образуется треугольник ABC, у которого угол при вершине B равен внешнему углу при вершине A. Это дано по условию: были даны равные углы при секущей.

Сумма углов в треугольнике равна 180°. Если угол треугольника при вершине B равен x градусов, то два остальных угла треугольника в сумме равны 180 – x.

Так как угол B треугольника равен внешнему углу A, то значит A также равен x градусов. Внутренний угол A и внешний угол A треугольника в сумме составляют 180°, так как это смежные углы. Тогда мы получаем, что внутренний угол A треугольника равен 180 – x. Но этого быть не может, так как 180 – x является суммой углов A и C треугольника.

Такое может быть только в случае, если угол C треугольника равен 0°. Однако такого быть не может, так как в этом случае отрезки AC и BC наложились бы друг на друга. То есть прямая a совпала бы с прямой b. Однако по условию даны разные прямые.

Таким образом доказано, что если накрест лежащие углы равны, то прямые пересекаться не могут. А если прямые не имеют точек пересечения, то они параллельны.