Диагональ делит угол пополам

Одним из признаков ромба является то, что диагонали делят его углы пополам. В виде теоремы этот признак формулируется так:

Если диагональ параллелограмма делит его угол пополам, то такой параллелограмм является ромбом.

Если доказывать данный признак, то нам дан параллелограмм, одна диагональ которого делит один угол пополам. Требуется доказать, что у такого параллелограмма будут равны все стороны (именно этот факт является определением ромба).

Пусть дан ромб ABCD, его диагональ BD делит угол B пополам: ∠ABD = ∠CBD.

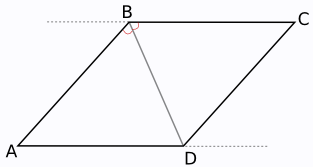
Как известно, в параллелограмме противоположные стороны параллельны. В данном случае AD || BC. Для этих прямых диагональ BD является секущей. Следовательно, ∠ABD = ∠CDB и ∠CBD = ∠ADB как накрест лежащие.

Но поскольку по условию ∠ABD = ∠CBD, то значит, что и углы при вершине D равны друг другу. Таким образом, доказано, что если диагональ параллелограмма делит один угол пополам, то она делит пополам и противоположный угол.

Оказывается, что все четыре угла, образованные диагональю в углах параллелограмма, равны друг другу. То есть в данном случае, не только накрест лежащие, но и односторонние углы при параллельных прямых тоже равны.

Рассмотрим треугольник ABD. В нем углы B и D равны. Значит, это треугольник равнобедренный с основанием BD. Так как у равнобедренных треугольников боковые стороны равны друг другу, то в данном случае AB = AD. Таким образом, доказано, что если диагональ делит угол параллелограмма пополам, то пара соседних сторон параллелограмма равна друг другу.

Но, как известно, у параллелограмма противоположные стороны не только параллельны друг другу, но и равны друг другу. Следовательно, AB = CD и AD = BC, а поскольку AB = AD, то все четыре стороны равны друг другу. Таким образом, доказано, что если диагональ делит угол параллелограмма пополам, то все стороны параллелограмма равны друг другу. А параллелограмм с равными сторонами является ромбом.