Доказать, что высота равнобедренного треугольника является биссектрисой и медианой

Существует теорема о том, что в равнобедренном треугольнике проведенная к его основанию высота также является биссектрисой и медианой. Доказать эту теорему можно следующим образом.

Представим равнобедренный треугольник ABC с боковыми сторонами AB и BC и основанием AC. Проведем в нем высоту BD.

Отметим, следующие факты:

• Отрезок BD перпендикулярен отрезку AC по построению.
• Точка D делит отрезок AC на два отрезка — AD и CD. Если доказать равенство этих отрезков, то это будет значить, что проведенная к основанию высота BD также является медианой к основанию равнобедренного треугольника.
• Отрезок BD создает в треугольнике два угла — ∠ABD и ∠CBD. Если доказать их равенство, то можно будет сделать вывод, что высота BD также является биссектрисой угла, противоположного основанию равнобедренного треугольника.

Создадим копию ∆ABC. Перевернем ее так, чтобы боковые стороны AB и BC поменялись местами. То есть перевернем копию треугольника на 180° вокруг оси BD.

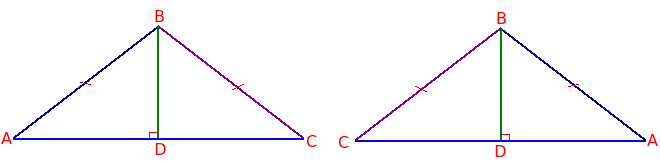
А теперь представим, что мы совмещаем эти треугольники. Поскольку стороны AB и BC равны, то они попарно совместятся. Поскольку ∠BAC и ∠BCA равны, то они также попарно совместятся. Совместятся и стороны AC треугольников и их углы B, так как это одна и та же сторона и угол. Таким образом оба треугольника полностью совместятся.

Теперь вспомним про высоту BD. Совместятся ли высоты двух наложенных треугольников? Если они совместятся, то это будет значить, что отрезок AD равен отрезку CD. Ведь второй треугольник перевернут, и CD находится на месте AD.

Существует теорема: из точки, не лежащей на прямой, можно провести только один перпендикуляр к прямой.

У треугольников точка B совместилась. У них же совместилось основание AC. То есть мы имеем дело с одной и той же точкой и с одной и той же прямой (отрезком) для двух треугольников. А по теореме существует только один перпендикуляр. Значит высота BD обоих треугольников совместилась, и значит AD = CD, следовательно BD является также медианой.

Также делается вывод, что ∠ABD и ∠CBD совмещаются и равны друг другу. Значит BD — является и биссектрисой.