Диагонали перпендикулярны

Одним из признаков ромба является то, что его диагонали взаимно перпендикулярны. В виде теоремы данный признак формулируется так:

Если диагонали параллелограмма перпендикулярны друг другу, то такой параллелограмм является ромбом.

Доказательство этой теоремы сводится к тому, чтобы доказать, что у такого параллелограмма стороны равны. Именно равенство сторон параллелограмма позволяет заключить, что это ромб.

Таким образом, нам дан параллелограмм, у которого диагонали взаимно перпендикулярны. Требуется доказать, что у такого параллелограмма все стороны равны.

Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E и перпендикулярны друг другу.

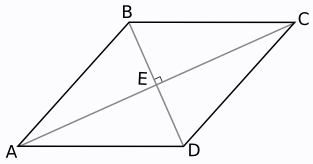
Одним из признаков параллелограмма является то, что его диагонали точкой пересечения делятся пополам. Поскольку нам дан параллелограмм, то AE = EC и BE = ED.

Рассмотрим треугольники AEB, BEC, CED, DEA. Все они прямоугольные, так как все углы при вершине E прямые, что дано по условию (диагонали перпендикулярны друг другу). У всех этих треугольников катеты также равны, так как являются половинками диагоналей. Таким образом, данные треугольники равны друг другу по двум сторонам и углу между ними или по двум катетам.

Из равенства треугольников следует равенство их соответствующих сторон и углов. Стороне AB треугольника ABE соответствуют стороны BC, CD, DA остальных треугольников. Значит, AB = BC = CD = DA.

Таким образом было доказано, что если в параллелограмме диагонали взаимно перпендикулярны, то его стороны равны, а значит, он является ромбом.